Bitcoin and Blockchain

Bitcoin graph

The European Commission stated in a report published in 2013, that their cyber security polls have concluded that in response to the current online security problems; 38% of European internet users have modified their internet behavior, 18% became less likely to make online purchases and 15% are now more reluctant to use internet banking. The report also revealed that 74% of the participants believed that the risk of being affected by cybercrime has risen, 12% were already affected by cybercrime in a way or another and 89% refrained from disclosing their personal information online. All this reveals a great demand for cryptography to secure not only electronic payments but also personal communications.

A group of researchers suggested a zero knowledge proof (ZKP) protocol that is based on the problem of graph isomerism. The proposed protocol can be used in creation of a cryptocurrency, just like bitcoin, and can also be used in encryption of data and securing communications.

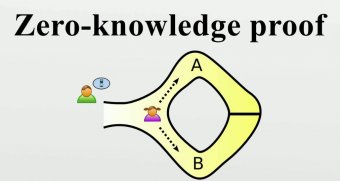
What is a Zero-knowledge Proof (ZKP) System?

Bitcoin is an example of a Zero-knowledge proof (ZKP) system which eliminated the need for a middleman, or a third party, to confirm transactions. ZKP allows the prover, or the spender, to convince the verifier, or the miner, of the validity of a statement, or a transaction, without having to reveal any information beyond that included within the statement, or transaction, to be verified.

The Suggested ZKP Protocol Which Is Based On the Graph Isomerism Problem:

The researchers proposed a ZKP that is based on the graph isomerism problem in the following manner:

Let’s assume 2 isomorphic graphs G1 and G2 so that G2 = L (G1) where graphs G1 and G2 represent the public key and the private key is represented by the isomorphism

1- The prover, or the spender, will randomly select an integer ϵ {0, 1}. In other words, he/she will toss a coin

2- The prover, or the spender, will select a random permutation and then formulates a new graph where G3 = μ (Ga)

3- The prover, or the spender, will then send the graph’s adjacency matrix which is G3 to the verifier, or the miner.

4- The verifier, or the miner, will then send a random integer ϵ {0, 1} to the prover, or the spender, and challenges him/her for λ which maps G3 to Gb

5- If the value of equals that of , the prover, or the miner, will send λ = μ-1to the verifier or, the spender.

6- If a = 0 and b = 1, the prover, or the spender, will send λ = μ-1 * L to the verifier, or the miner.

7- If a = 1 and b = 0, the prover, or the spender, will send λ = to the verifier, or the miner.

8- The verifier, or the miner, will check if λ (G3 ) () and if confirmed will grant access to the prover, or confirm the transaction of the spender.

Repeated rounds of these mathematical operations need to be executed for the verifier, or the miner, to confirm that the prover, or the spender, is the real owner of the private keys related to the statement, or transaction in question, given the fact that the prover can occasionally be lucky enough to the guess the value of before G3 is successfully sent. The probability of occurrence of this can be estimated by the following function with representing the number of rounds. Accordingly, with several rounds taking place, the innate probability of this instance is relatively low, and probability of the verifier, or the miner, to confirm the identity of the prover, or the spender, is measured by the “level of confidence” which is calculated by the following function 1 – .

Accordingly, the presented protocol provides a zero-knowledge proof (ZKP) based on the problem of graph isomerism while promoting integrity, soundness and zero knowledge.