Introduction to Bitcoin mining
Proof of work
Cryptographer Adam Back realized in 1997 that it was possible to use hash functions to prove that you did a certain amount of computational work. His discovery took advantage of the special property of strong cryptographic hashes where each hash looks like random data regardless of what input was used to create it.
For example, the main hash in Bitcoin produces a 256-bit output, which means that it’s output is similar in randomness to flipping 256 coins in sequence and recording each heads as a 0 and each tails as a 1.
So if you create two hashes from two different inputs, you would expect (on average) that the first bit of one of those hashes would be a 0 (“heads”). That means a hash starting with a zero bit is proof that you did the computational work (“number of coin flips”) necessary to create (on average) two hashes.
Extending this, a hash starting with a zero byte (8 zero bits, or “8 heads”, in a row) is proof you did the computational work (on average) to create 256 hashes.
The nice thing about hashes rather than coin flips is that it’s possible for anyone else in the world to verify you did the work by simply hashing the same input data you used with the same hash function. It doesn’t matter whether it took 256 hashes or 256 trillion hashes to get your result, anyone else in the world can verify it by doing a single hash.
Each block header contains the hash of the previous block. Remember that changing any input totally changes the hash output. This means that if block header 2 contains the hash of block 1’s header, block 1’s header can’t be changed without making block 2 no longer link to it.
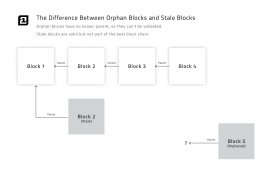
Bitcoin requires that every block header link to a previous block header back to the first block (called the Genesis block). If a Bitcoin program can’t verify the link between a block header and its parent block header, it considers that block invalid (called an orphan block).
(We'll discuss stale blocks below in the Header Chain Forks section.)
This means that proof of work in Bitcoin is cumulative. The proof of work (average number of hashes) demonstrated by block header 2 adds to the proof of work demonstrated by block header 1. A block header 3 that linked to block header 2 would further increase that accumulated proof of work.
When a header has a single child, it’s considered to be confirmed once. If that child header has its own child header, the original header has two confirmations, and so on. As of this writing, the first block header, created in January 2009, has more than 380, 000 confirmations, demonstrating more proof of work than the current fastest supercomputer in the world could generate in a million years.
This link between block header 2 and block header 1 is called a header chain. A link from block header 3 to block header 2 would extend that chain.
Every Bitcoin client looks for the best header chain: the chain of valid block headers that has the most cumulative proof of work. We’ll describe why this chain is treated specially in a moment.
Some resources, even Satoshi Nakamoto’s original Bitcoin paper, incorrectly describe this special chain as “the longest chain”; but since different headers can demonstrate different amounts of proof of work, what matters is the cumulative proof of work, not the number of headers chained together.
Mining
The process of generating proof of work for block headers is called mining, so named because the people who create the first 6.93 million bitcoin blocks receive newly-minted bitcoins as a reward for their work, similar to how gold miners receive gold for their work.
Based on the bitcoin inflation graph by TheRealSteve, which was released under the CC0 public domain grant
Recall from above that the output hash for a particular piece of input data seems random the first time you generate that hash. This means it's not possible to predict when a miner will produce a header with the amount of proof of work necessary to add that header to the best header chain. As a consequence, mining is competitive—a large miner who can create hashes twice as fast as a smaller miner will add twice as many headers to the chain, but the smaller miner will still add half that number of hashes and receive roughly half the compensation—so if the smaller miner has a better profit margin than the larger miner, the smaller miner could still be better off.